O que é?
A Dinâmica dos Fluídos Computacional ou CFD, é a área que trata da simulação numérica de escoamentos de fluidos, transferência de calor e fenômenos relacionados.
As simulações numéricas representam um arranjo de vários esquemas numéricos dedicados a resolver problemas como: equações algébricas, sistemas de equações lineares, interpolar e ajustar pontos, derivadas e integrais, equações diferenciais ordinárias etc.
Os fluídos são governados por equações diferenciais parciais (EDP)[1] que representam as leis de conservação da massa, quantidade de movimento e energia.
A Dinâmica dos Fluidos Computacional (CFD) é a substituição desses sistemas de equações (EDP) por um conjunto de equações algébricas que podem ser resolvidas usando computadores. O CFD teve origem a partir da combinação de duas disciplinas: a mecânica dos fluidos, o cálculo numérico e a tecnologia dos computadores.
Mecânica dos fluidos
A mecânica dos fluidos, nesse âmbito, volta-se ao comportamento de fluidos em repouso e em movimento, e às forças agindo sobre esses sistemas. A história mostra que os estudos mais importantes nessa área são datados do século XIII, do final do século XIX e início do século XX.
A “Hydrodynamica” de 1738, escrito por Daniel Bernoulli, “Princípios gerais do movimento dos fluidos” de 1757 de Leonhard Euler, primeira tentativa de modelar um fluido, a “teoria da camada limite” apresentada por Ludwig Prandtl, em 1904, um marco referencial nesse contexto. Outros como Reynolds, Froude, Von Kármán, Navier, Stokes e Mach dedicaram seus estudos a esses fenômenos e são nomes comuns nos textos desta área.
A mecânica dos fluidos, neste contexto, está dentro de uma parte da mecânica conhecida como ciências térmicas a qual envolve sistemas para a armazenagem, a transferência e a conversão de energia. Vista dessa forma, a mecânica dos fluidos pode parecer algo muito etéreo e de pouca aplicação prática fora da academia. Contudo, se observarmos o nosso entorno, veremos a mecânica dos fluidos em quase tudo que encontramos no nosso campo de visão. O ar escoando e “pesando” sobre nossas cabeças, a água escoando por tubulações, o gás escoando nos trocadores de calor ou sendo comprimido e expandido nos refrigeradores domésticos e comerciais.
- Uma equação diferencial parcial ou equação de derivadas parciais (EDP) é uma equação envolvendo funções de várias variáveis independentes e dependente de suas derivadas. Estas equações surgem naturalmente em problemas de física matemática, física e engenharia.
O desenvolvimento tecnológico só é possível pelo conhecimento das leis que governam os processos e pelo controle e supervisão deles.
Cálculo numérico
O engenheiro interessado em resolver um determinado problema tem a sua disposição basicamente três ferramentas:
– Os métodos analíticos;
– Os métodos numéricos (simulação numérica);
– As experimentações empíricas em laboratório ou em campo.
Os métodos analíticos têm a desvantagem de serem aplicados apenas a problemas cujas hipóteses simplificativas os desviam demasiadamente do fenômeno físico real e, geralmente, só podem ser aplicados para geometrias simples. Nem por isso as soluções analíticas são descartadas, pois são muito importantes para validar casos-limites de modelos numéricos. Além disso, a solução é do tipo fechada, definitiva para aquela situação.
A grande vantagem da experimentação em laboratório é o fato de se tratar com a configuração real, podendo-se verificar novos fenômenos. No entanto, o seu custo, normalmente elevado, e, às vezes, de impossível execução, como por exemplo para a transferência de calor no núcleo de reatores nucleares ou reentrada de veículos na atmosfera.
Os métodos numéricos correspondem a um conjunto de ferramentas ou métodos matemáticos usados para se obter a solução de problemas de forma aproximada. Esses métodos se aplicam principalmente a problemas que não apresentam uma solução exata, portanto, precisam ser resolvidos numericamente por aproximação.
Quando se trabalha com estes métodos numéricos deve-se ter noção da essência de um método numérico. À diferença em relação às soluções analíticas, devem ser avaliadas as situações em que eles devem ser aplicados; as vantagens de se utilizar um método numérico, as limitações na sua aplicação e a confiabilidade na solução obtida.
Tecnologia dos computadores
Hoje, ao resolver um problema de fluido dinâmica, usando soluções numéricas, o mais comum é o uso de um pacote computacional aliado a computadores especializados ou workstation de uso pessoal. Isto ocorre devido ao aumento contínuo da capacidade de computação disponível, o desenvolvimento de métodos numéricos por diversos pesquisadores, e softwares específicos que tornaram a simulação computacional de problemas matemáticos uma prática usual nas mais diversas áreas científicas e tecnológicas.
Equações governantes dos escoamentos
A solução das equações de Navier Stokes era bastante difícil até a invenção de computadores realmente rápidos. Era tão difícil que matemáticos, físicos e engenheiros se restringiram a atalhos e aproximações. Mas, observando o que um “fluido real” é capaz de fazer, tinha que ser difícil (Stewart, 2013).
Abaixo as equações governantes na forma bidimensionais:
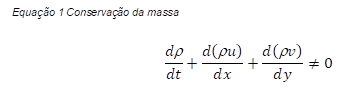



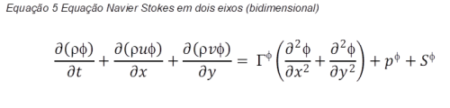
A equação de governo dos escoamentos na forma genérica:

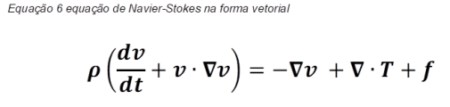

Na esquerda do sinal de igual temos a aceleração de uma região do fluido e, no termo da direita, são as forças que agem sobre ele: pressão, tensão, momento angular, momento linear etc.
O ponto (.) é uma operação com vetores, e V é uma expressão em derivadas parciais:
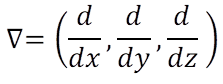
O problema tridimensional
Embora estas equações tenham sido escritas no século 19, ainda não foi comprovado que nas três dimensões existem sempre soluções ou que, se elas existem, então não contêm qualquer singularidade (Fefferman, 2019). Existe um prêmio de U$ 1.000.000,00 que foi oferecido em maio de 2000 pelo Instituto de Matemática Clay[2] para qualquer um que fizer progressos substanciais na direção de uma teoria matemática que possa ajudar a entender este fenômeno.
Equação Navier Stokes resolvida via CFD
A equação resolvida via CFD é a equação de transporte da variável de interesse, representada pelo símbolo Φ.
A equação é apresentada abaixo:

Todas as equações de conservação resolvidas em CFD possuem a forma acima, com quatro termos: o termo de tempo, o termo advectivo[3], o termo difusivo e o termo fonte.
Para representar diferentes equações de conservação, alteram-se apenas três componentes da equação: a variável Φ, o coeficiente de difusão Γ e o termo fonte S.
Por exemplo, para a equação de conservação de massa (ou contínuo), a variável Φ é igual a 1, o coeficiente de difusão e a fonte são nulos. Apesar da fórmula ser amplamente utilizada para aplicações em CDF, pode-se afirmar que, até o momento, não existe solução analítica da equação acima.
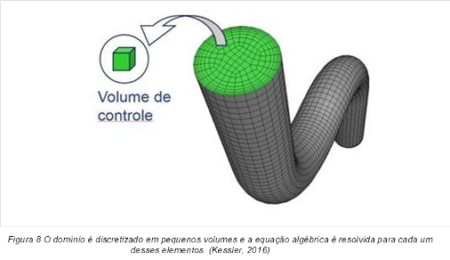
Dessa forma, é necessário reescrevê-la em forma algébrica e resolvê-la por meio de algum método de discretização[4], malha computacional conforme a figura 1.
Os métodos de discretização mais difundidos são:
– método das diferenças finitas;
– método dos elementos finitos;
– método dos volumes finitos.
Inicialmente, resolvia-se os problemas de escoamento empregando o método de diferenças finitas, enquanto o método de elementos finitos era empregado na solução de problemas de mecânica dos sólidos. Mas uma das limitações do método de diferenças finitas, se não a principal, é a não execução do “balanço de massa” local nos volumes do domínio. Logo, a massa era uma variável inconsistente nos resultados das simulações.
Por outro lado, no método de elementos finitos, apesar da versatilidade geométrica, característica notável desta metodologia, pois, a geometria pode possuir forma, cargas e condições de contorno arbitrárias, é difícil a obtenção de um “operador” para minimizar a variável “massa”, de forma que essa, geralmente, também não é conservada localmente.
Portanto, os métodos de elementos finitos e diferenças finitas possuem limitações no uso em CFD que vêm sendo investigadas já a algumas décadas por matemáticos e engenheiros.
Os métodos de volumes finitos e volumes de controle surgiram com a finalidade de executar o balanço de massa local no domínio de cálculo, em que ele se faz necessário. Pode-se dizer que o método de volumes finitos é oriundo do de diferenças finitas e que o método de volume de controle provém dos de volumes finitos e elementos finitos.
Todos os métodos utilizados para resolver escoamentos tendem para:
– solução de escoamentos sobre geometrias complexas;
– conservação das propriedades do fluído localmente;
– economia de tempo computacional.
Com esses métodos, troca-se o domínio contínuo por um domínio discreto, onde um conjunto de volumes de controle é utilizado para representar o domínio original, como pode ser observado na figura 2.

figura 2
A forma algébrica da equação apresentada anteriormente é resolvida em cada um dos volumes de controle, gerando um sistema de equações que deve ser resolvido numericamente. O número de volumes de controle a ser usado para a análise deve ser estabelecido por meio do estudo de convergência de malha, ou seja, analisa-se o mesmo caso com malhas de refinamentos diferentes e comparam-se os resultados. Quando o resultado entre dois refinamentos de malha não sofre alteração (ou muda muito pouco), diz-se que a convergência de malha foi atingida.
Com a malha gerada, passa-se à configuração da física do modelo, das condições de contorno e do solver. Depois disso, resolve-se o sistema de equações através de um processo interativo, até a convergência, ou seja, quando a variação dos resultados entre duas interações consecutivas ficar abaixo de um critério estabelecido pelo usuário.
A etapa final é a de pós-processamento, quando os resultados são avaliados por meio de ferramentas como vetores, linhas de corrente, distribuições de cores, planos de corte, isosuperfícies etc.
Para que serve?
A necessidade de aplicar aproximações numéricas decorre do fato de que esses problemas podem se mostrar intratáveis se dispomos apenas de meios puramente analíticos, como aqueles estudados nas disciplinas cálculo diferencial e integral e álgebra linear.
A maioria dos problemas envolvendo fenômenos reais de fluido dinâmica produzem modelos matemáticos cuja solução analítica é difícil (ou impossível) de obter, mesmo quando provamos que a solução existe.
Nas aplicações de aproximações numéricas para esses problemas apesar de, em geral, serem diferentes da solução exata, elas podem ser bem próximas. Porém, ele terá que tomar uma série de decisões antes de resolver o problema. E, para tomar essas decisões, é preciso ter conhecimento de métodos numéricos.
O profissional terá que decidir:
- Pela utilização ou não de um método numérico (existem métodos numéricos para se resolver este problema?);
- Escolher o método a ser utilizado, procurando aquele que é mais adequado para o seu problema;
- Que vantagens cada método oferece e que limitações eles apresentam;
- Saber avaliar a qualidade da solução obtida. Para isso, é importante ele saber exatamente o que está sendo feito pelo computador ou calculadora, isto é, como determinado método é aplicado.
Aplicações de CFD na engenharia
A Dinâmica dos Fluidos Computacional pode ser utilizada desde a fase conceitual de um projeto, auxiliando a determinar a viabilidade e qual a melhor solução em produto até a etapa de produção, permitindo representar diversos cenários.
Com o auxílio das ferramentas de CFD é possível:
– Simular difusão e convecção de substâncias fluidas nos mais diferentes ambientes, como salas de cirurgias, átrios, salas limpas etc.;
– Analisar a aerodinâmica e a aerotermodinâmica de veículos;
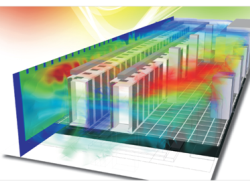
– Avaliar a refrigeração de equipamentos, como datacenter e microeletrônica, motores etc.;
– Fazer estudos de caracterização de poluição ambiental, dispersão de gases (fumaça), análise e simulação de lançamento de poluentes e contaminantes;
– Simular hidrodinâmica e hemodinâmica;
– Testar e desenvolver projetos de sistemas propulsivos e de geração de energia em geral.
Análises com o uso CFD, alguns exemplos
Resultados bidimensionais – Duto
O escoamento no interior de um duto convergente, conforme mostra a figura. 3. A malha utilizada contém 31×14 células e o escoamento foi resolvido para as equações de Euler.
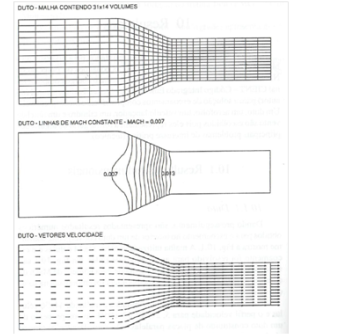
Figura 3
Na figura. 4 são mostradas ainda as linhas de Mach constante para número de Mach da corrente livre 0,007. Neste caso, a metodologia foi empregada na solução de escoamentos incompressíveis.

figura 4

Figura 5
Nas figuras 4 e 5 são apresentados a malha de 44×36 células e o perfil velocidade para 5,27,50, 73 e 95% do comprimento de um duto constituído de placas paralelas. São considerados os termos viscosos presentes nas equações de Navier-Stokes.
Desta forma, o perfil de velocidade e do tipo parabólico simétrico com comprimento de L ,5 vezes a sua altura.
Resultados tridimensionais – túnel de vento
O túnel de vento, por exemplo, contém uma secção de 1×1 metros quadrados e 9,5 metros de comprimento, sendo 2,4 metros de secção de teste.
A malha apresentada na figura 6 possui 65x11x11 células e foi obtida com concentração nas proximidades dos cantos da secção do túnel.

Figura 6
Mostra-se ainda as linhas de Mach constante e os vetores de velocidade obtidos para Mach da corrente livre 0,05 no interior do túnel, considerando as equações de Euler. As linhas de Mach constante são aproximadamente paralelas e possuem valores que variam entre 0,05 e 0,01. Espera-se um valor de Mach 0,04 na saída do túnel e 0,01 na secção maior do mesmo, conforme mostram as figuras 6 e 7
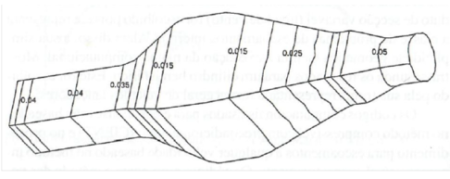
figura 7
Na figura 7 verifica-se que as linhas de Mach constante apresentam algumas oscilações, principalmente no duto difusor. Isto deve-se, provavelmente, a pequenas variações de velocidade que não foram eliminadas para um critério de convergência e= 10-4
A figura 8 mostra que os vetores velocidade calculados são correntes para as equações de Euler (não considera a viscosidade do fluido). Para as equações de Navier-Stokes, por outro lado, as velocidades seriam nulas nas paredes do túnel.
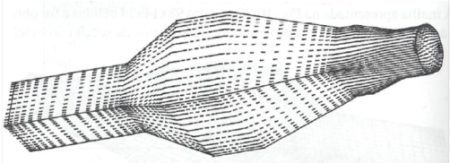
Figura 8
Resultados numéricos e experimentais mostram que o projeto do túnel deve ser reavaliado (reprojetado). São sugeridas algumas modificações:
- aumento da relação área/comprimento da seção de teste;
- transformação da insuflação em sucção;
- diminuição dos ângulos de abertura dos bocais para evitar descolamento da camada limite.
Softwares de Dinâmica dos Fluidos Computacional
Na atualidade existem diferentes ferramentas que auxiliam os profissionais de engenharia a realizar análises de Fluidodinâmica Computacional. Alguns são pacotes multifásicos, que combinam a simulação de propriedades mecânicas, térmicas, elétricas e fluido mecânicas em uma única interface e permite desenvolver um projeto completo, do desenho à simulação e análise dos resultados.
Porém, também existem ferramentas com foco exclusivo nas soluções de CFD que permitem realizar diferentes análises, como: turbulência, transferência de calor, reações químicas, aero acústica, turbo máquinas, modelar o fluxo de fluidos etc..
Figura 9 – Resultado tridimensionais – Data Center
Figura 10 – Sala limpa em instalações farmacéuticas

Resultados tridimensionais – Data center
Por que usar?
O CFD é uma alternativa oportuna e econômica para as análises empíricas e teste de fluxo de fluidos. No entanto, em vez de competir com as análises empíricas, o CFD é frequentemente usado em uma função complementar. Por exemplo, a avaliação final do projeto pode depender de testes físicos limitados após uma extensa avaliação de CFD para reduzir o número de designs prospectivos durante a fase de concepção do projeto.
Os túneis de vento e outras formas de testes físicos geralmente usam modelos em escala para análise de fluxo, e sempre há necessidade de fatores de correção empíricos para imitar os resultados em escala total. Em contraste, o CFD pode simular o fluxo de ar em um difusor ou duto, sem a necessidade de fatores de correção, usando um modelo CAD digital de tamanho completo, conforme demonstra a Figura 11.

Figura 11
O CFD pode produzir todos os resultados que se esperaria de testes físicos (por exemplo, levantamento, arrasto e perda de pressão). Além disso, também fornece fácil acesso a campos de fluxo (por exemplo, velocidade, pressão), em superfícies e dentro do volume do fluido para visualização de fluxo 3D.
Figura 12 – Inserção de mercado de Cfd 9por % de usuários) em 2011 e 2017

A democratização do CFD
No artigo The democratization of CFD, o Dr. Eng. R. K. Hanna e o Dr. Eng. I. Weinhold da Mentor Graphics Corp., fazem uma previsão diante do atual quadro mundial de usuários de CFD:
[…] É inteiramente concebível que um dia nossos netos – ou digamos que daqui a duas gerações de engenheiros – achem graça de nós quando dissermos que passamos dois terços do nosso tempo criando geometria e malhas para fazer simulação de fluidodinâmica com CFD[…]
[…] E nós realmente gastamos dias e semanas no pré-processamento, quando eles serão capazes de fazer CFD “em tempo real” com o toque de uma tela? Ou talvez eles façam simulações de fluido, calor e análise de transferência de massa diretamente de seus cérebros enquanto usam algum dispositivo ou capacete! […]
[…] A democratização, o uso intensivo, deve ser uma consequência da maneira como os engenheiros projetam produtos e procuram soluções para seus problemas […]
[…] A democratização dos CFDs é de fato possível, mas é necessário passar dos 5-10% de penetração de mercado para 80-90% nos próximos 30-40 anos e isto exigirá mais reflexão do atual quadro e provavelmente repensar radicalmente as estruturas de código de CFD com pesquisas mais fundamentais nas universidades e empresas. […]
Bibliografia
Boche, A. (2005). Metodos Numericos. Porto Alegre: Editora da UFRGS.
Bortoli, A. L. (2000). Dr. Eng. Mecanico. Porto Alegre: Editora da UFRGS.
Dr. Eng. R.K. Hanna e Dr. Eng. I. Weinhold. (03 de 2017). The democratization of CFD. Mentor Graphics Corp. – Whitepaper Mechanical Analysis, 01 – 22. Fonte: www.mentor.com.
Fefferman, C. L. (11 de 06 de 2019). Existence and smoothness of the Navier–Stokes equation. Fonte: Clay Reasearch: http://claymath.org/millennium/Navier-Stokes_Equations/navierstokes.pdf
Kessler, M. (2016). Dr. Eng. Mecanico. Fonte: blog Esss: https://www.esss.co/blog/fluidodinamica-computacional-o-que-e/
Mentor Graphics Corporation. (17 de 05 de 2019). HVAC and Buildings. Fonte: www.mentor.com: https://www.mentor.com/products/mechanical/industries/build-hvac
Stewart, I. (2013). 17 Equações que mudaram o mundo. São Paulo: Jorge Zahar Editores.
Zikanov, O. (2010). Essential Computational Fluid Dynamics. Dearborn: Wiley Editora.
Anderson Rodrigues, engenheiro, projetor e consultor, é diretor da Artécnica